離散数学
aを正の整数とし,b=a²とする。aを2進数で表現するとnビットであるとき,bを2進数で表現すると最大で何ビットになるか。
- n+1
- 2n
- n²
- 2ⁿ
A,B,C,Dを論理変数とするとき,次のカルノー図と等価な論理式はどれか。ここで,・は論理積,+は論理和,XはXの否定を表す。
| CD | 00 | 01 | 11 | 10 | |
| AB | |||||
| 00 | 1 | 0 | 0 | 1 | |
| 01 | 0 | 1 | 1 | 0 | |
| 11 | 0 | 1 | 1 | 0 | |
| 10 | 0 | 0 | 0 | 0 | |
- A・B・C・D+B・D
- A・B・C・D+B・D
- A・B・D+B・D
- A・B・D+B・D
浮動小数点数を,仮数部が7ビットである表示形式のコンピュータで計算した場合,情報落ちが発生しないものはどれか。ここで,仮数部が7ビットの表示形式とは次のフォーマットであり,( )₂内は2進数,Yは指数である。また,{ }内を先に計算するものとする。
- {(1.1)₂×2⁻³+(1.0)₂×2⁻⁴}+(1.0)₂×2⁵
- {(1.1)₂×2⁻³-(1.0)₂×2⁻⁴}+(1.0)₂×2⁵
- {(1.0)₂×2⁵+(1.1)₂×2⁻³}+(1.0)₂×2⁻⁴
- {(1.0)₂×2⁵-(1.0)₂×2⁻⁴}+(1.1)₂×2⁻³
全体集合S内に異なる部分集合AとBがあるとき,A∩Bに等しいものはどれか。ここで,A∪BはAとBの和集合,A∩BはAとBの積集合,AはSにおけるAの補集合,A−BはAからBを除いた差集合を表す。
- A−B
- (A∪B)−(A∩B)
- (S−A)∪(S−B)
- S−(A∩B)
任意のオペランドに対するブール演算Aの結果とブール演算Bの結果が互いに否定の関係にあるとき,AはBの(又は,BはAの)相補演算であるという。排他的論理和の相補演算はどれか。
- 等価演算
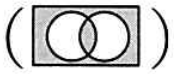
- 否定論理和
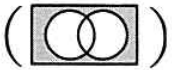
- 論理積
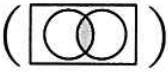
- 論理和
桁落ちによる誤差の説明として,適切なものはどれか。
- 値のほぼ等しい二つの数値の差を求めたとき,有効桁数が減ることによって発生する誤差
- 指定された有効桁数で演算結果を表すために,切捨て,切上げ,四捨五入などで下位の桁を削除することによって発生する誤差
- 絶対値が非常に大きな数値と小さな数値の加算や減算を行ったとき,小さい数値が計算結果に反映されないことによって発生する誤差
- 無限級数で表される数値の計算処理を有限項で打ち切ったことによって発生する誤差
正の整数の10進表示の桁数Dと2進表示の桁数Bとの関係を表す式のうち,最も適切なものはどれか。
- D ≒ 2log10B
- D ≒ 10log2B
- D = Blog210
- D ≒ Blog102
あるホテルは客室を1,000部屋もち,部屋番号は,数字4と9を使用しないで0001から順に数字4桁の番号としている。部屋番号が0330の部屋は,何番目の部屋か。
- 204
- 210
- 216
- 218
0以上255以下の整数nに対して,
と定義する。next(n)と等しい式はどれか。ここで,x AND y 及び x OR y は,それぞれxとyを2進数表現にして,桁ごとの論理積及び論理和をとったものとする。
- (n + 1) AND 255
- (n + 1) AND 256
- (n + 1) OR 255
- (n + 1) OR 256
論理和(∨),論理積(∧),排他的論理和(⊕)の結合法則の成立に関する記述として,適切な組合せはどれか。
| (A∨B)∨C =A∨(B∨C) |
(A∧B)∧C =A∧(B∧C) |
(A⊕B)⊕C =A⊕(B⊕C) |
|
| ア | 必ずしも成立しない | 成立する | 成立する |
| イ | 成立する | 必ずしも成立しない | 成立する |
| ウ | 成立する | 成立する | 必ずしも成立しない |
| エ | 成立する | 成立する | 成立する |
応用数学
製品100個を1ロットとして生産する。一つのロットからサンプルを3個抽出して検査し,3個とも良品であればロット全体を合格とする。100個中に10個の不良品を含むロットが合格と判定される確率は幾らか。
- 178/245
- 405/539
- 89/110
- 87/97
M/M/1の待ち行列モデルにおいて,窓口の利用率が25%から40%に増えると,平均待ち時間は何倍になるか。
- 1.25
- 1.60
- 2.00
- 3.00
非線形方程式f(x)=0の近似解法であり,次の手順によって解を求めるものはどれか。ここで,y=f(x)には接線が存在するものとし,(3)でx₀と新たなx₀の差の絶対値がある値以下になった時点で繰返しを終了する。
〔手順〕
(1)解の近くの適当なx軸の値を定め,x₀とする。
(2)曲線y=f(x)の,点(x₀, f(x₀))における接線を求める。
(3)求めた接線と,x軸の交点を新たなどのとし,手順(2)に戻る。
- オイラー法
- ガウスの消去法
- シンプソン法
- ニュートン法
ATM(現金自動預払機)が1台ずつ設置してある二つの支店を統合し,統合後の支店にはATMを1台設置する。統合後のATMの平均待ち時間を求める式はどれか。ここで,待ち時間はM/M/1の待ち行列モデルに従い,平均待ち時間にはサービス時間を含まず,ATMを1台に統合しても十分に処理できるものとする。
〔条件〕
(1)統合後の平均サービス時間:Ts
(2)統合前のATMの利用率:両支店ともρ
(3)統合後の利用者数:統合前の両支店の利用者数の合計
3台の機械A,B,Cが良品を製造する確率は,それぞれ60%,70%,80%である。機械A,B,Cが製品を一つずつ製造したとき,いずれか二つの製品が良品で残り一つが不良品になる確率は何%か。
- 22.4
- 36.8
- 45.2
- 78.8
通信回線を使用したデータ伝送システムにM/M/1の待ち行列モデルを適用すると,平均回線待ち時間,平均伝送時間,回線利用率の関係は,次に式で表すことができる。
回線利用率が0%から徐々に増加していく場合,平均回線待ち時間が平均伝送時間よりも最初に長くなるのは,回線利用率が幾つを超えたときか。
- 0.4
- 0.5
- 0.6
- 0.7
コンピュータによる伝票処理システムがある。このシステムは,伝票データをためる待ち行列をもち,M/M/1の待ち行列モデルが適用できるものとする。平均待ち時間がT秒以上となるのは,処理装置の利用率が少なくとも何%以上となったときか。ここで,伝票データをためる待ち行列の特徴は次のとおりである。
・伝票データは,ポアソン分布に従って到着する。
・伝票データをためる数に制限はない。
・1件の伝票データの処理時間は,平均T秒の指数分布に従う。
- 33
- 50
- 67
- 80
受験者1,000人の4教科のテスト結果は表のとおりであり,いずれの教科の得点分布も正規分布に従っていたとする。90点以上の得点者が最も多かったと推定できる教科はどれか。
| 教科 | 平均点 | 標準偏差 |
| A | 45 | 18 |
| B | 60 | 15 |
| C | 70 | 8 |
| D | 75 | 5 |
- A
- B
- C
- D
相関係数に関する記述のうち,適切なものはどれか。
- すべての標本点が正の傾きを持つ直線上にあるときは,相関係数が+1になる。
- 変量間の関係が線形の時は,相関係数が0になる。
- 変量間の関係が非線形の時は,相関係数が負になる。
- 無相関の時は,相関係数が−1になる。
(1 + α)nの計算を,1 + n × α で近似計算ができる条件として,適切なものはどれか。
- |α| が1に比べて非常に小さい。
- |α| が n に比べて非常に大きい。
- |α ÷ n| が1より大きい。
- |n × α| が1より大きい。
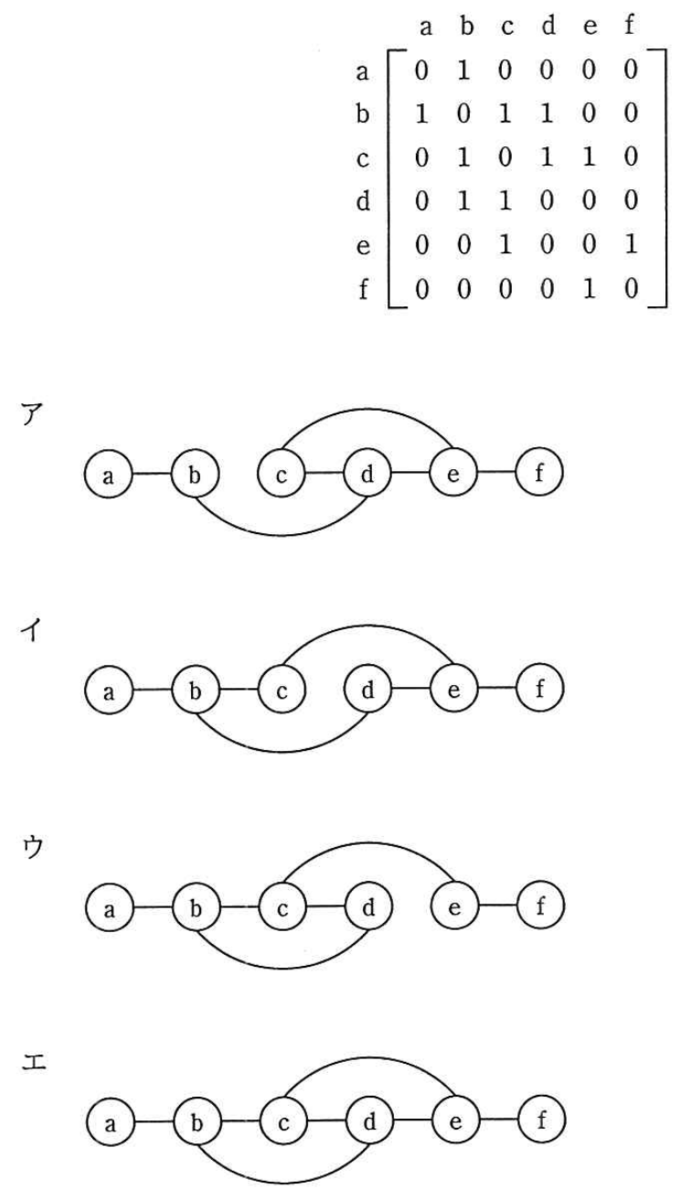
ノードとノードの間のエッジの有無を,隣接行列を用いて表す。ある無向グラフの隣接行列が次の場合,グラフで表現したものはどれか。ここで,ノードを隣接行列の行と列に対応させて,ノード間にエッジが存在する場合は1で,エッジが存在しない場合は0で示す。
次の数式は,ある細菌の第n世代の個数f(n)が1世代後にどのように変化するかを表現したものである。この漸化式の解釈として,1世代後の細菌の個数が,第n世代と比較してどのようになるかを説明しているものはどれか。
- 1世代後の個数は,第n世代の個数の1.8倍に増える。
- 1世代後の個数は,第n世代の個数の2.2倍に増える。
- 1世代後の個数は,第n世代の個数の2倍になり,更に増殖後の20%が増える。
- 1世代後の個数は,第n世代の個数の2倍になるが,増殖後の20%が死ぬ。
情報に関する理論
AIにおける過学習の説明として,最も適切なものはどれか。
- ある領域で学習した学習済みモデルを,別の領域に再利用することによって,効率的に学習させる。
- 学習に使った訓練データに対しては精度が高い結果となる一方で,未知のデータに対しては精度が下がる。
- 期待している結果とは掛け離れている場合に,結果側から逆方向に学習させて,その差を少なくする。
- 膨大な訓練データを学習させても効果が得られない場合に,学習目標として成功と判断するための報酬を与えることによって,何が成功か分かるようにする。
AIにおけるディープラーニングに最も関連が深いものはどれか。
- 試行錯誤しながら条件を満たす解に到達する方法であり,場合分けを行い深さ優先で探索し,解が見つからなければ一つ前の場合分けの状態に後戻りする。
- 神経回路網を模倣した方法であり,多層に配置された素子とそれらを結ぶ信号線で構成され,信号線に付随するパラメタを調整することによって入力に対して適切な解が出力される。
- 生物の進化を模倣した方法であり,与えられた問題の解の候補を記号列で表現して,それを遺伝子に見立てて突然変異,交配,とう汰を繰り返して逐次的により良い解に近づける。
- 物質の結晶ができる物理現象を模倣した方法であり,温度に見立てたパラメタを制御して,大ざっぱな解の候補から厳密な解の候補に変化させる。
式A+B×Cの逆ポーランド表記法による表現として,適切なものはどれか。
- ×+ABC
- ×+ABC
- ABC×+
- CBA+×
a,b,c,dの4文字から成るメッセージを符号化してビット列にする方法として表のア〜エの4通りを考えた。この表はa,b,c,dの各1文字を符号化するときのビット列を表している。メッセージ中でのa,b,c,dの出現頻度は,それぞれ50%,30%,10%,10%であることが分かっている。符号化されたビット列から元のメッセージが一意に復号可能であって,ビット列の長さが最も短くなるものはどれか。
| a | b | c | d | |
| ア | 0 | 1 | 00 | 11 |
| イ | 0 | 01 | 10 | 11 |
| ウ | 0 | 10 | 110 | 111 |
| エ | 00 | 01 | 10 | 11 |
AIの機械学習における教師なし学習で用いられる手法として,最も適切なものはどれか。
- 幾つかのグループに分かれている既存データ間に分離境界を定め,新たなデータがどのグループに属するかはその分離境界によって判別するパターン認識手法
- 数式で解を求めることが難しい場合に,乱数を使って疑似データを作り,数値計算をすることによって解を推定するモンテカルロ法
- データ同士の類似度を定義し,その定義した類似度に従って似たもの同士は同じグループに入るようにデータをグループ化するクラスタリング
- プロットされた時系列データに対して,曲線の当てはめを行い,得られた近似曲線によってデータの補完や未来予測を行う回帰分析
AIにおけるディープラーニングに関する記述として,最も適切なものはどれか。
- あるデータから結果を求める処理を,人間の脳神経回路のように多層の処理を重ねることによって,複雑な判断をできるようにする。
- 大量のデータからまだ知られていない新たな規則や仮説を発見するために,想定値から大きく外れている例外事項を取り除きながら分析を繰り返す手法である。
- 多様なデータや大量のデータに対して,三段論法,統計的手法やパターン認識手法を組み合わせることによって,高度なデータ分析を行う手法である。
- 知識がルールに従って表現されており,演繹手法を利用した推論によって有意な結論を導く手法である。
次に示す記述は,BNFで表現されたあるプログラム言語の構文の一部である。<パラメタ指定>として,適切なものはどれか。
<パラメタ指定>::=<パラメタ>|(<パラメタ指定>, <パラメタ>)
<パラメタ>::=<英字>|<パラメタ><英字>
<英字>::=a|b|c|d|e|f|g|h|i
- ( (abc,def), ghi)
- ( (abc, def) )
- (abc, (def) )
- (abc)
符号化方式に関する記述のうち,ハフマン方式はどれか。
- 0と1の数字で構成する符号の中で,0又は1の連なりを一つのブロックとし,このブロックに長さを表す符号を割り当てる。
- 10進数字の0~9を4ビット2進数の最初の10個に割り当てる。
- 発生確率が分かっている記号群を符号化したとき,1記号当たりの平均符号長が最小になるように割り当てる。
- 連続した波を標本化と量子化によって0と1の数字で構成する符号に割り当てる。
表は,文字A~Eを符号化したときのビット表記と,それぞれの文字の出現確率を表したものである。1文字当たりの平均ビット数は幾らになるか。
| 文字 | ビット表記 | 出現確率(%) |
| A | 0 | 50 |
| B | 10 | 30 |
| C | 110 | 10 |
| D | 1110 | 5 |
| E | 1111 | 5 |
- 1.6
- 1.8
- 2.5
- 2.8
次のBNFにおいて非終端記号から生成される文字列はどれか。
- 123
- 124
- 127
- 128
四つのアルファベットa~d から成るテキストがあり,各アルファベットは2ビットの固定長2進符号で符号化されている。このテキストにおける各アルファベットの出現確率を調べたところ,表のとおりであった。各アルファベットの符号を表のような可変長2進符号に変換する場合,符号化されたテキストの,変換前に対する変換後のビット列の長さの比は,およそ幾つか。
| アルファベット | a | b | c | d |
| 出現確率(%) | 40 | 30 | 20 | 10 |
| 可変長2進符号 | 0 | 10 | 110 | 111 |
- 0.75
- 0.85
- 0.90
- 0.95
UTF-8の説明に関する記述として,適切なものはどれか。
- 1文字を1バイトから4バイト(又は6バイト)までの可変長で表現しており,ASCIIと上位互換性がある。
- 2バイトで表現する領域に収まらない文字は,上位サロゲートと下位サロゲートを組み合わせて4バイトで表現する。
- ASCII文字だけを使用することが前提の電子メールで利用するために,7ビットで表現する。
- 各符号位置が4バイトの固定長で表現される符号化形式である。
あるプログラム言語において,識別子(identifier)は,先頭が英字で始まり,それ以降に任意個の英数字が続く文字列である。これをBNFで定義したとき,a に入るものはどれか。
<digit>::=0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
<letter>::=A | B | C | … | X | Y | Z | a | b | c | … | x | y | z
<identifier>::= a
- <letter> | <digit> | <identifier><letter> | <identifier><digit>
- <letter> | <digit> | <letter><identifier> | <identifier><digit>
- <letter> | <identifier><digit>
- <letter> | <identifier><digit> | <identifier><letter>
通信に関する理論
ハミング符号とは,データに冗長ビットを付加して, 1ビットの誤りを訂正できるようにしたものである。ここでは,X₁,X₂,X₃,X₄の4ビットから成るデータに,3ビットの冗長ビットP₃,P₂,P₁を付加したハミング符号 X₁X₂X₃P₃X₄P₂P₁ を考える。付加ビットP₁,P₂,P₃は,それぞれ
X₁ ⊕ X₃ ⊕ X₄ ⊕ P₁ = 0
X₁ ⊕ X₂ ⊕ X₄ ⊕ P₂ = 0
X₁ ⊕ X₂ ⊕ X₃ ⊕ P₃ = 0
となるように決める。ここで⊕は排他的論理和を表す。
ハミング符号 1110011 には1ビットの誤りが存在する。誤りビットを訂正したハミング符号はどれか。
- 0110011
- 1010011
- 1100011
- 1110111
図のように16ビットのデータを4×4の正方形状に並べ,行と列にパリティビットを付加することによって何ビットまでの誤りを訂正できるか。ここで,図の網掛け部分はパリティビットを表す。
| 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 |
- 1
- 2
- 3
- 4
計測・制御に関する理論
サンプリング周波数40kHz,量子化ビット数16ビットでA/D変換したモノラル音声の1秒間のデータ量は,何kバイトとなるか。ここで, 1kバイトは1,000バイトとする。
- 20
- 40
- 80
- 640
体温を測定するのに適切なセンサはどれか。
- サーミスタ
- 超音波センサ
- フォトトランジスタ
- ポテンショメータ
組込みシステムにおけるリアルタイムシステムにおいて,システムへの入力に対する応答のうち,最も適切なものはどれか。
- OSを使用しないで応答する。
- 定められた制限時間内に応答する。
- 入力された順序を守って応答する。
- 入力時刻を記録して応答する。
家庭用ゲーム機に採用され,自動車の先端運転支援システムにも使われる距離画像センサの一つである,TOF(Time of Flight)方式のセンサの説明として,適切なものはどれか。
- 光源から射出されたレーザなどの光が,対象物に反射してセンサに届くまでの時間を利用して距離を測定する。
- ステレオカメラによって,三角測量の原理を利用して距離を測定する。
- 単眼カメラによって,道路の幅や車線は無限遠の地平線で一点に収束するという遠近法の原理を利用して距離を測定する。
- 複数の衛星からの電波を受け取り,電波に含まれる情報から発信と受信の時刻差を求め,電波の伝播速度をかけることによって,各衛星との距離を割り出し,それを基に緯度及び経度を特定する。