ノードとノードの間のエッジの有無を,隣接行列を用いて表す。ある無向グラフの隣接行列が次の場合,グラフで表現したものはどれか。ここで,ノードを隣接行列の行と列に対応させて,ノード間にエッジが存在する場合は1で,エッジが存在しない場合は0で示す。
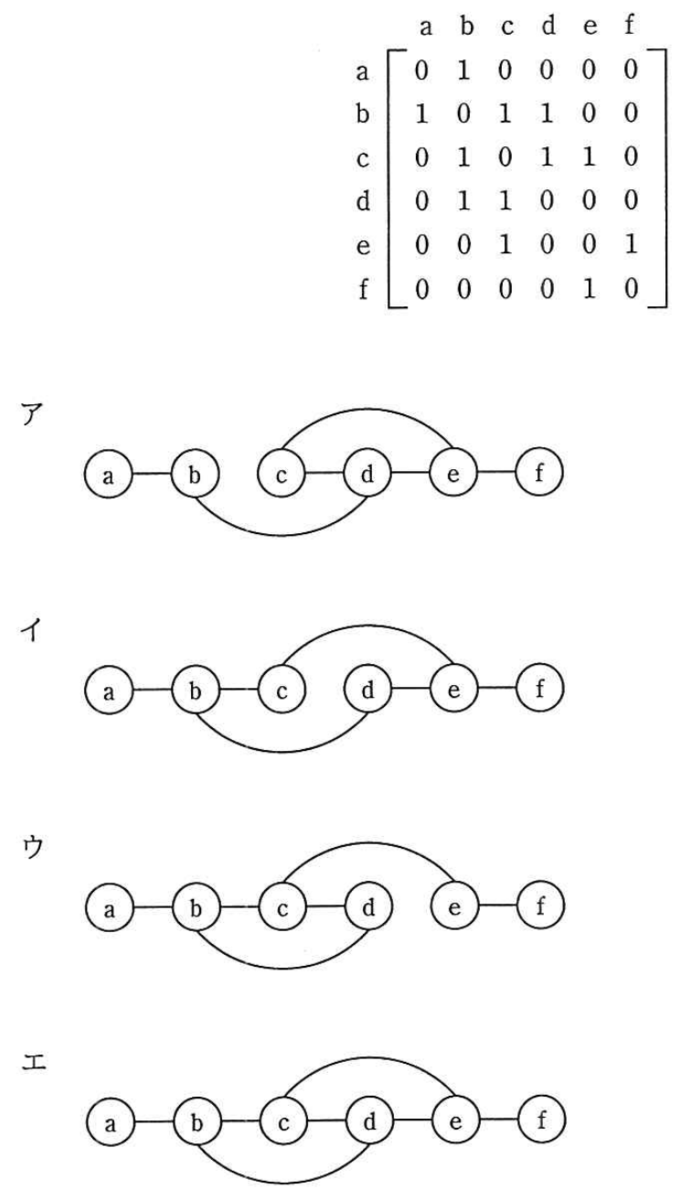
解答
ウ
解説
与えられた隣接行列から、ノード間にエッジが存在する(線がつながっている)組み合わせは、
(a, b)(b, c)(b, d)(c, d)(c, e)(e, f)
の5種類になります。
- (b, c)が接続していないため誤りです。
- (c, d)が接続していないため誤りです。
- 正しいです。
- (d, e)が接続しているため誤りです。
参考情報
分野・分類
| 分野 | テクノロジ系 |
| 大分類 | 基礎理論 |
| 中分類 | 基礎理論 |
| 小分類 | 応用数学 |
出題歴
- FE 令和元年度秋期 問3
- AP 平成29年度春期 問3