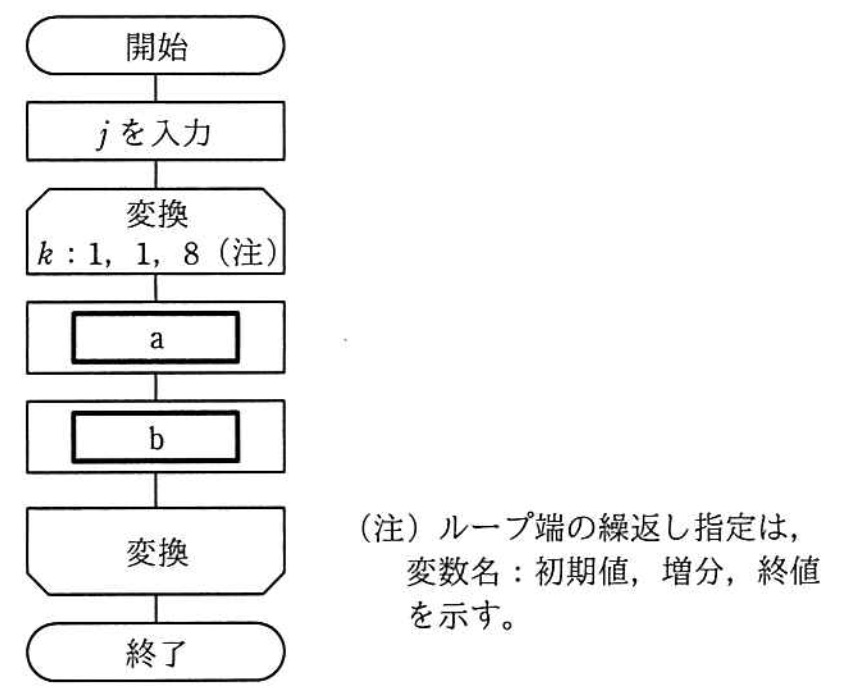
次の流れ図は,10進整数j(0<j<100)を8桁の2進数に変換する処理を表している。2進数は下位桁から順に,配列の要素NISHIN(1)からNISHIN(8)に格納される。流れ図のa及びbに入れる処理はどれか。ここで,j div 2 はjを2で割った商の整数部分を,j mod 2 はiを2で割った余りを表す。
| a | b | |
| ア | j ← j div 2 | NISHIN(k) ← j mod 2 |
| イ | j ← j mod 2 | NISHIN(k) ← j div 2 |
| ウ | NISHIN(k) ← j div 2 | j ← j mod 2 |
| エ | NISHIN(k) ← j mod 2 | j ← j div 2 |
解答
エ
解説
一般的な2進数変換のアルゴリズムです。
まず、2進数の1桁目(NISHIN(1))を求めるには、10進数を2で割った余り(j mod 2)を求めます。
次に、2進数の2桁目(NISHIN(1))を求めるには、10進数を2で割った商(j div 2)について、2で割った余り(j mod 2)を求めます。
これを繰り返していきます。
具体的に“99”という10進数を2進数に変換する場合は例に挙げると、流れは次の通りになります。
- 1桁目 j mod 2 = 1、NISHIN(1) ← 1、j div 2 = 49、j←49
- 2桁目 j mod 2 = 1、NISHIN(2) ← 1、j div 2 = 24、j←24
- 3桁目 j mod 2 = 0、NISHIN(3) ← 0、j div 2 = 12、j←12
- 4桁目 j mod 2 = 0、NISHIN(4) ← 0、j div 2 = 6、j←6
- 5桁目 j mod 2 = 0、NISHIN(5) ← 0、j div 2 = 3、j←3
- 6桁目 j mod 2 = 1、NISHIN(6) ← 1、j div 2 = 1、j←1
- 7桁目 j mod 2 = 1、NISHIN(7) ← 1、j div 2 = 0、j←0
- 8桁目 j mod 2 = 0、NISHIN(8) ← 0、j div 2 = 0、j←0
よって、10進数の99は、2進数の01100011になるとわかります。
この処理を行なっている式は、エです。
参考情報
分野・分類
| 分野 | テクノロジ系 |
| 大分類 | 基礎理論 |
| 中分類 | 基礎理論 |
| 小分類 | 離散数学 |
出題歴
- FE 令和元年度秋期 問1