QC検定3級 相関分析②

◀︎ 前へ｜次へ ▶︎️

　散布図に関する次の文章において，　　　内に入るもっとも適切なものを下欄の選択肢からひとつ選べ。ただし，各選択肢を複数回用いることはない。

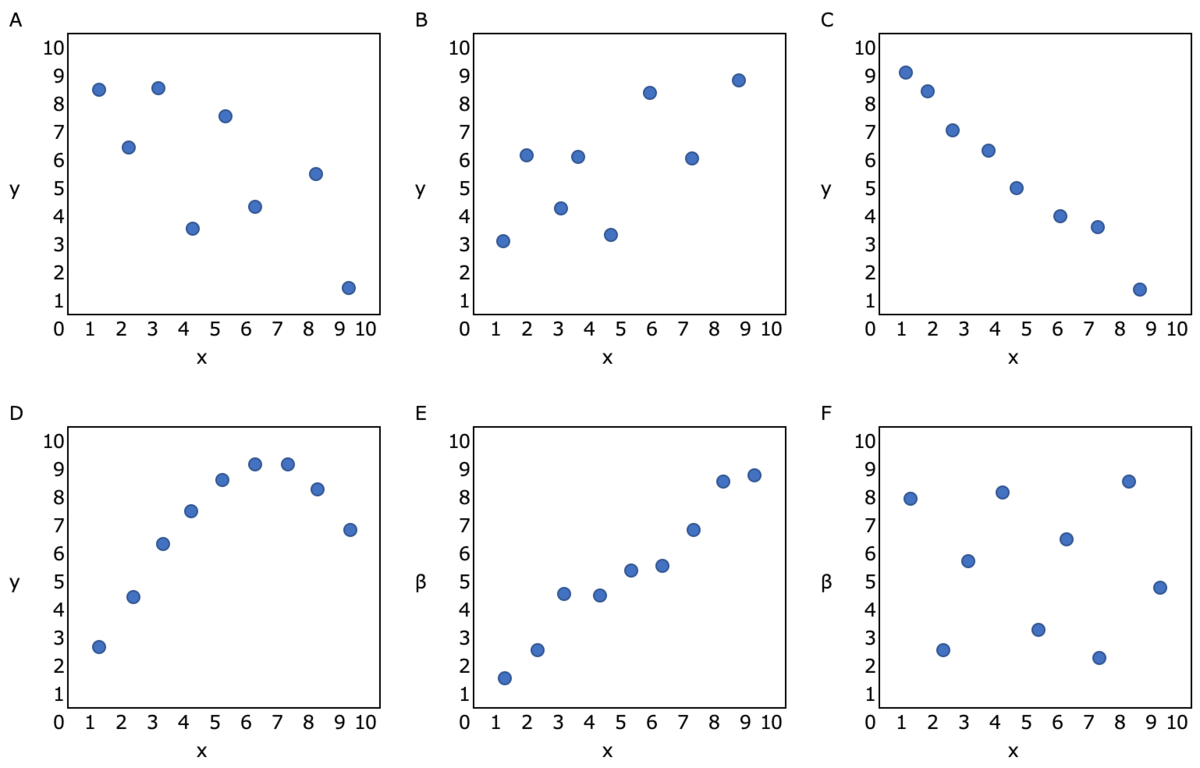
①　次図A〜Fはそれぞれ対応するデータx，yに対する散布図である。それぞれの散布図から読み取れるxとyの関係は，図A： （1） ，図B： （2） ，図C： （3） ，図D： （4） ，図E： （5） ，図F： （6） である。

②　図Aのx，yのデータとその補助表を次表に示す。これより，xの偏差平方和S_xx，yの偏差平方和S_yy，xとyの偏差積和S_xyを求めると，
　S_xx =  （7） 　，S_yy =  （8） 　，S_xy =  （9） 
となる。これより相関係数rは，r =  （10） となる。

No	x	y	x2	y2	x×y
1	1	8	1	64	8
2	2	6	4	36	12
3	3	8	9	64	24
4	4	4	16	16	16
5	5	7	25	49	35
6	6	4	36	16	24
7	8	5	64	25	40
8	9	1	81	1	9
合計	38	43	236	271	168

（1）〜（6）の選択肢

1. 正の相関がある
2. 強い正の相関がある
3. 負の相関がある
4. 強い負の相関がある
5. 曲線的な関係がある
6. 相関関係がない

（7）〜（10）の選択肢

1. 0.77
2. 0.23
3. −0.23
4. −0.77
5. −36.25
6. 36.25
7. 39.88
8. 55.50

解答・解説

解答

（1）	（2）	（3）	（4）	（5）
ウ	ア	エ	オ	イ
（6）	（7）	（8）	（9）	（10）
カ	ク	キ	オ	エ

参考書・問題集  

解説

①　次図A〜Fはそれぞれ対応するデータx，yに対する散布図である。それぞれの散布図から読み取れるxとyの関係は，図A：　負の相関がある　，図B：　正の相関がある　，図C：　強い負の相関がある　，図D：　曲線的な関係がある　，図E：　強い正の相関がある　，図F：　相関関係がない　である。

1. 右下がりに分布しており，負の相関があります。
2. 右上がりに分布しており，正の相関があります。
3. Aよりも直線的に右下がりに分布しており，強い負の相関があります。
4. x=7を境に正負の相関が異なり，曲線的な関係があります。
5. Bよりも直線的に右上がりに分布しており，正の相関があります
6. ばらついており相関関係は確認できません。

②　図Aのx，yのデータとその補助表を次表に示す。これより，xの偏差平方和S_xx，yの偏差平方和S_yy，xとyの偏差積和S_xyを求めると，
　S_xx = 　55.50　　，S_yy = 　39.88　　，S_xy = 　−36.25　
となる。これより相関係数rは，r = 　−0.77　となる。

　各計算式は次のとおりです。
　　S_xx = Σx² − (Σx)²/n = 236 − 38^2/8 = 55.5
　　S_yy = Σy² − (Σy)²/n = 271 − 43^2/8 = 39.875
　　S_xy = Σ(x×y)² − (Σx)(Σy)/n = 236 − 38^2/8 = −36.25
　　r = S_xy / (√S_xx × √S_yy) ≒ −0.77